
이번 포스팅에서는 다층신경망에서 경사하강법으로 가중치를 업데이트하는 원리를 다룬다.
단일신경망

이전 포스팅까지 다뤘던 예측 모델은 입력층과 출력층으로만 구성된 단일신경망이었다.
다층신경망
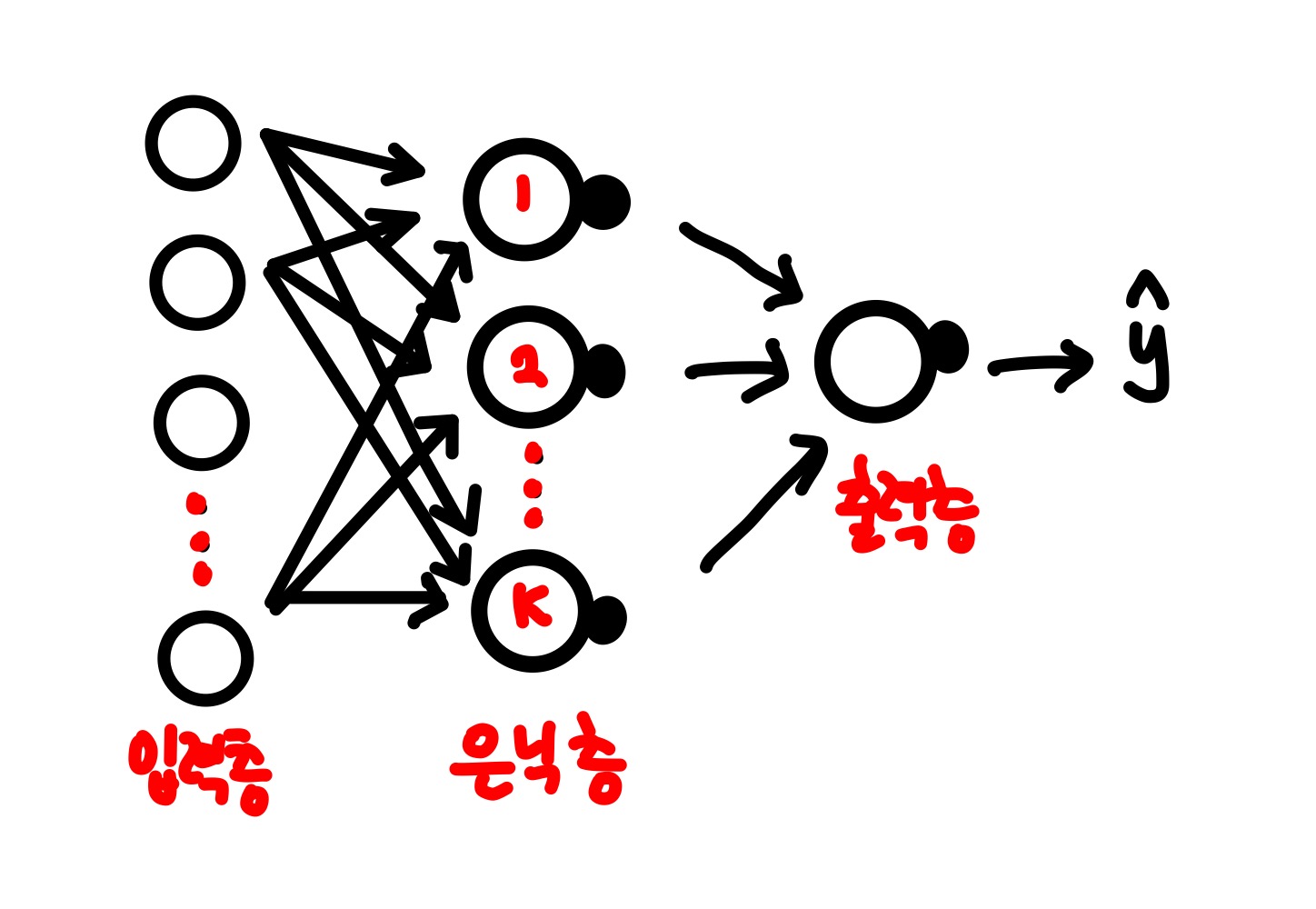
위 그림은 K개의 뉴런을 가진 다층신경망이다.
보통 입력층의 개수는 층의 개수에 포함시키지 않는다. 그래서 위와 같은 다층신경망을 2개의 층(은닉층, 출력층)을 가진 다층신경망이라고 한다. 위 그림에서 출력층의 뉴런은 1개인데, 내가 다룰 모델은 이진분류모델이기 때문에 은닉층의 각 뉴런에서 출력된 값을 하나의 뉴런으로 다시 모아야하기 때문이다. 다중분류모델이라면 출력층에 여러개의 뉴런이 존재할 수 있다.
경사하강법 적용하기

다층신경망을 단순화해서 그렸다. 경사하강법을 적용하기 위해서는 W2와 b2 그리고 W1,b1에 대한 손실함수 L의 도함수를 구한 후 가중치와 절편을 업데이트 해줘야한다. 그럼 하나씩 계산해보자.
STEP1. 행렬 크기 정리하기
계산하기에 앞서, X, W, b, Z등이 모두 행렬이기 때문에 각 행렬의 크기를 미리 정리해두면 계산시 편리하다. 입력층은 m개의 특성을 가진 n개의 샘플이고, 은닉층의 뉴런은 k개라고 가정하면 아래와 같이 각 인자의 행렬 사이즈를 정리할 수 있다.
| 입력층 --> 은닉층 | 은닉층 --> 출력층 | ||||
| X | |||||
| n * m | |||||
| W1 | + B1 | ||||
| m * k | n * m | ||||
| Z1 | A1 | ||||
| n * k | n * k | ||||
| W2 | +B2 | ||||
| k * 1 | n * 1 | ||||
| Z2 | A2 | Y | |||
| n * 1 | n * 1 | n * 1 | |||
STEP2. 도함수 계산
1. 가중치에 대한 손실함수의 도함수(출력층)

2. 가중치의 대한 손실함수의 도함수(은닉층)

3. 절편에 대한 손실함수의 도함수(출력층)

4. 절편에 대한 손실함수의 도함수(은닉층)

(오타 수정) B1 행렬의 크기는 n * m으로 봐야한다.
Conclusion.




다음 포스팅에서는 계산한 도함수를 가지고 가중치를 업데이트하는 다층신경망을 Python으로 구현해본다.
Reference.
도서 <Do it! 코딩으로 배우는 딥러닝 입문> 이지스 퍼블리싱, 박해선지음
끝.