
이번 포스팅에서는 이진분류 알고리즘 3가지를 알아본다.
먼저 이진분류의 개념에 대해서 짚고 넘어가자.
이진분류란 임의의 샘플 데이터를 True나 False로 구분하는 문제를 말한다.
예를 들어 특정 종양 샘플이 주어졌을 때 이 종양이 양성(True)인지 음성(False)인지 판단하는 것이 있다.
이진분류 알고리즘은 퍼셉트론 → 아달린 → 로지스틱 회귀 순으로 발전했다.
이번 포스팅에서 하나씩 살펴본다.
| 1. 퍼셉트론(Perceptron)
퍼셉트론은 1957년 코넬 항공 연구소의 프랑크 로젠블라트가 발표한 알고리즘으로,
이진분류 문제에서 최적의 가중치를 학습하는 알고리즘이다.
퍼셉트론의 구조를 도식화하면 아래와 같다.
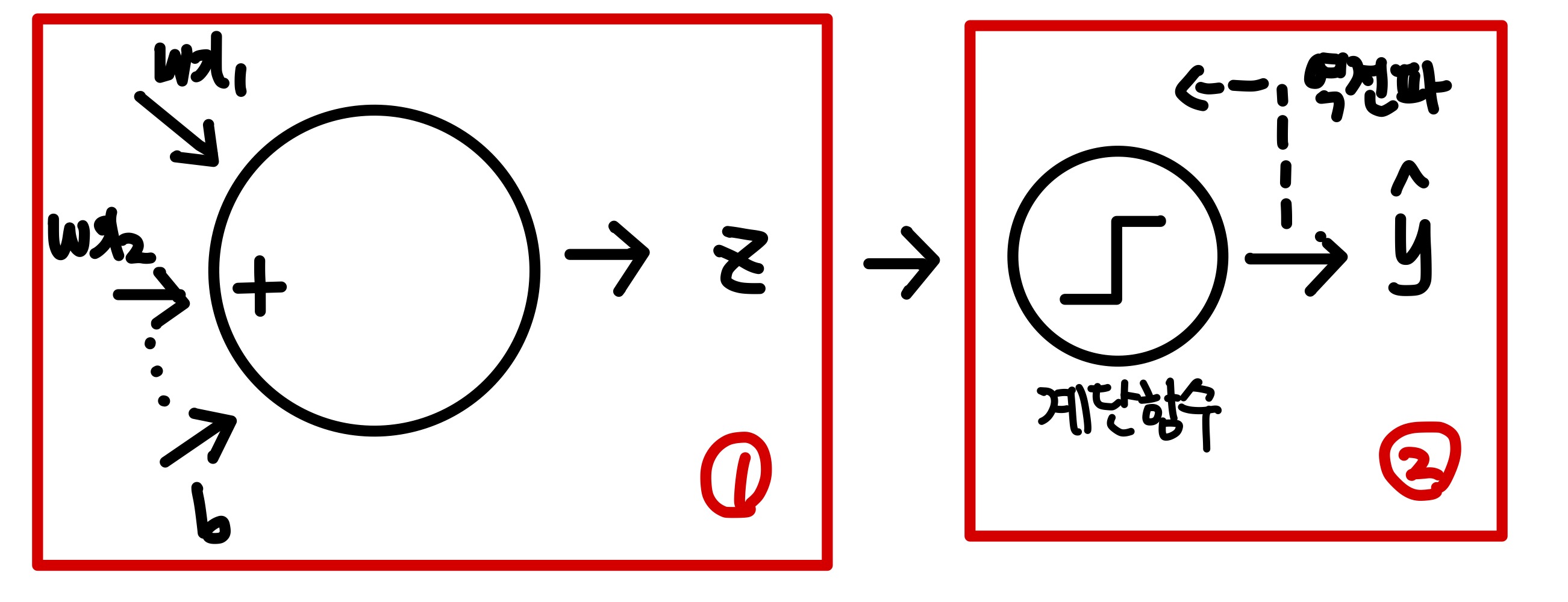
퍼셉트론 이전 포스팅에서 다뤘던 선형회귀 알고리즘과 유사하다.
선형회귀 알고리즘이 선형함수로만 이뤄져있었다면, 퍼셉트론은 선형함수 뒤에 계단함수가 붙은 모양이다.
*선형회귀 알고리즘에 대한 설명은 더보기 포스팅에서 확인할 수 있다.
① 선형함수
첫번째 동그라미는 선형함수이다.
가중치, 절편, 입력데이터 등의 입력신호들을 받아 z값을 만든다.
수식으로 정리하면 아래와 같다.
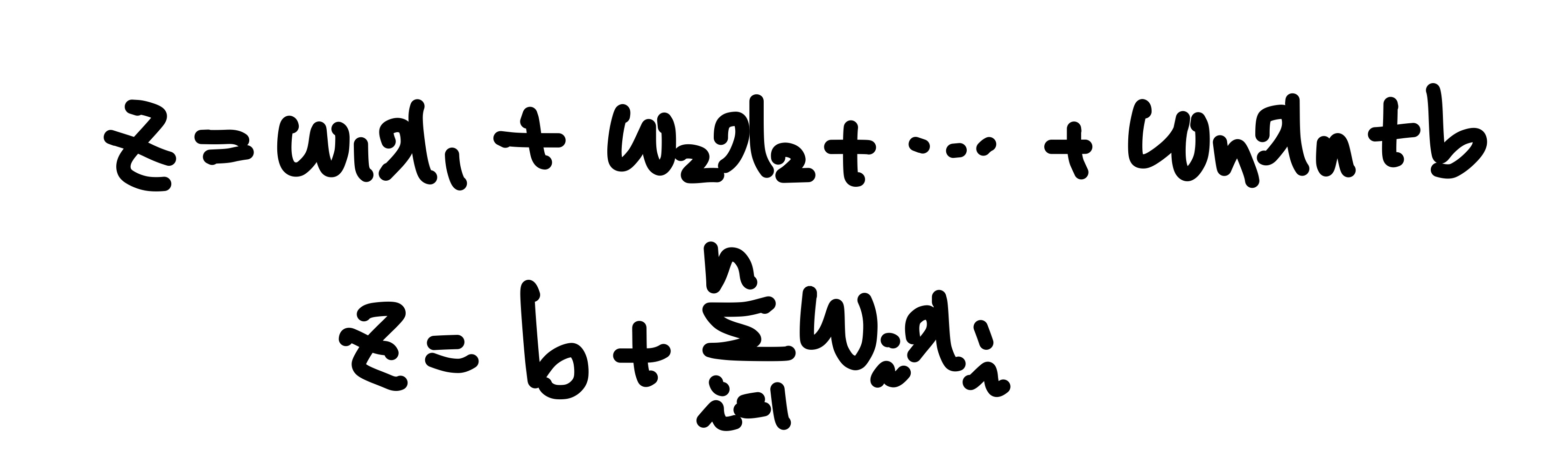
② 계단함수
두번째 동그라미는 계단함수이다.
계단함수는 z가 0보다 크면 1로, 0보다 작으면 -1로 분류한다.
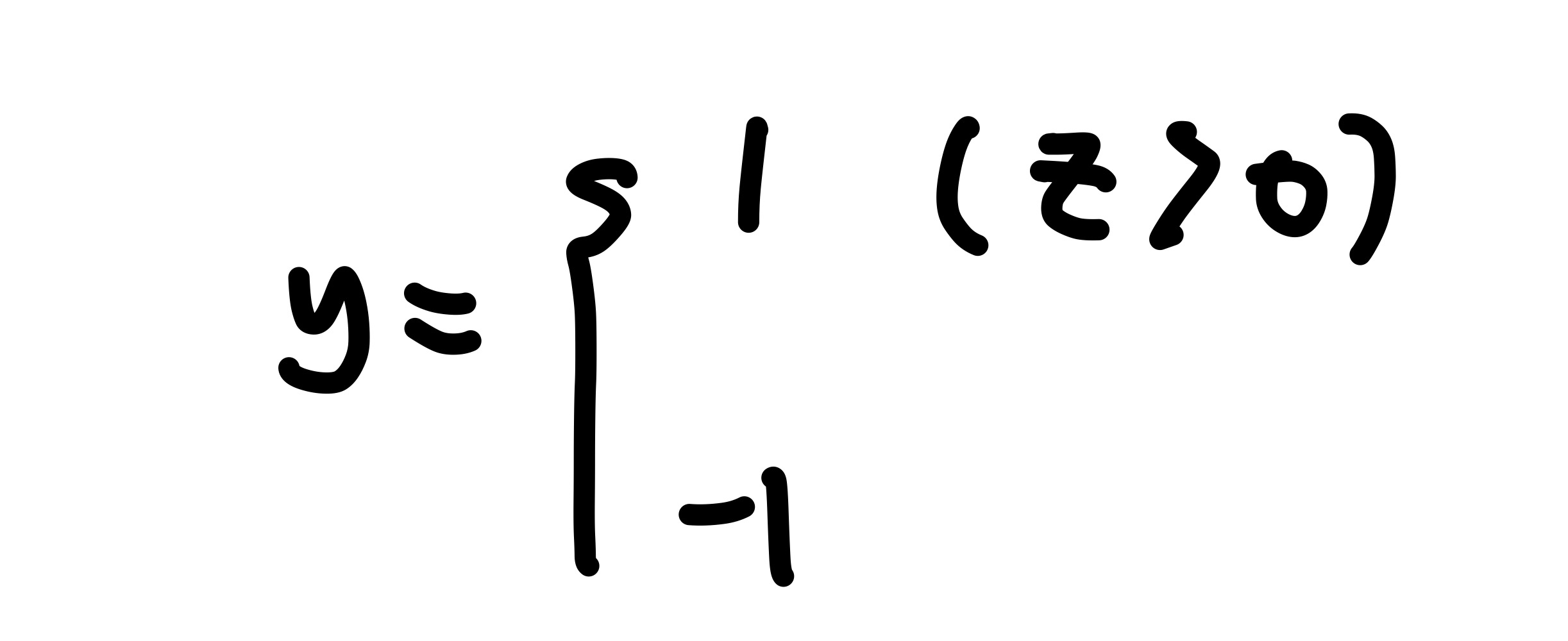
이때, 1을 양성클래스, -1을 음성 클래스라고 부른다.
그림으로 그리면 아래와 같아서 계단함수라고 부른다.

퍼셉트론은 계단함수의 결과를 사용하여 역전파가 진행된다(가중치와 절편의 업데이트).
정리하면 퍼셉트론은 선형함수를 통과한 값 z를 계단함수로 보내 0보다 큰지 작은지 검사하며 1 또는 -1로 분류하는 알고리즘이다.
| 2. 아달린(Adalin)
아달린은 1960년에 스탠포드 대학의 버나드 위드로우와 테드호프가 퍼셉트론을 개선한 적응형 선형뉴런(Adaptive Linear Neuron)의 줄임말이다.
아달린과 퍼셉트론의 차이는 퍼셉트론은 계단함수의 결과를 가중치 업데이트에 사용했지만
아달린은 선형함수의 결과를 사용한다는 점이다.
도식화하면 아래와 같다.
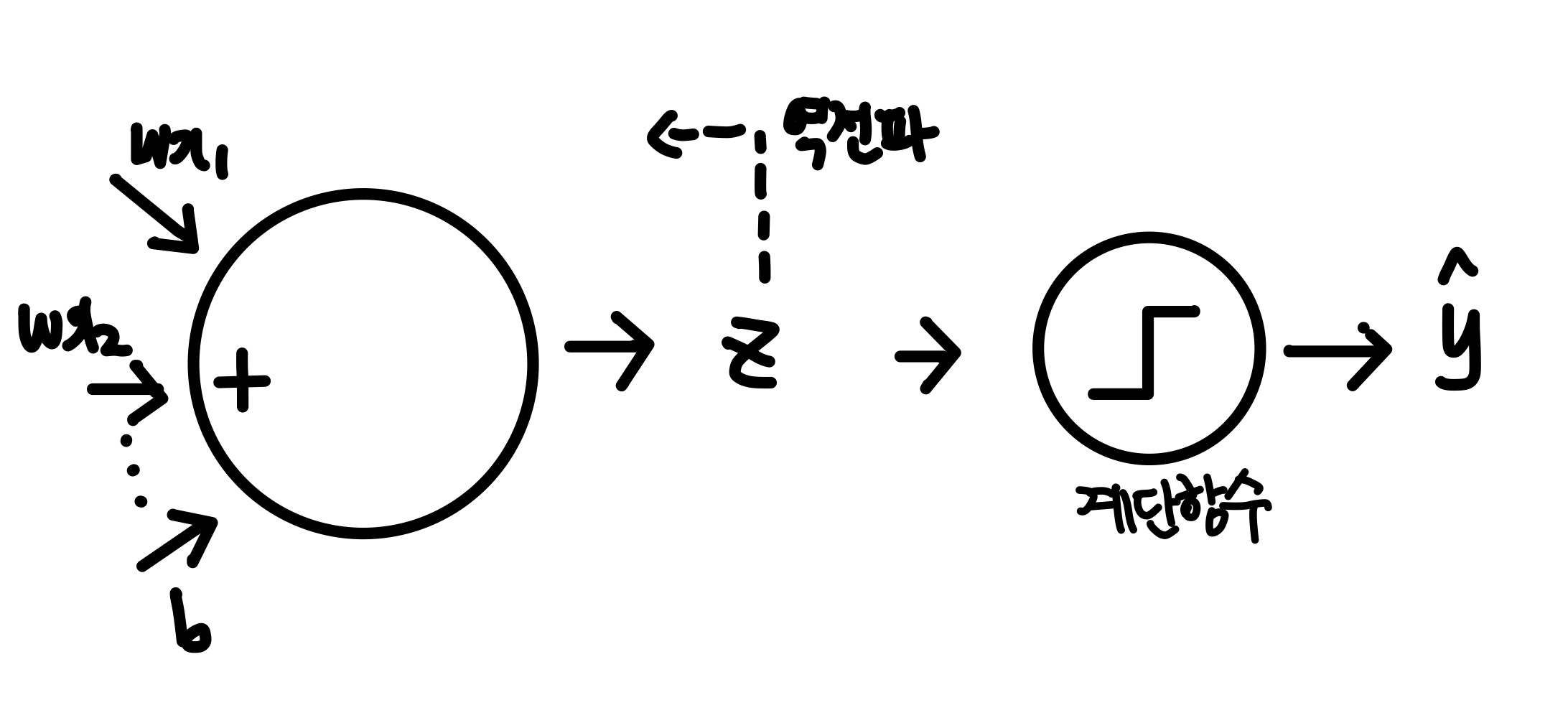
| 3. 로직스틱 회귀(Logistic Regression)
로지스틱 회귀는 이름이 회귀이지만 분류알고리즘이다.
아달린에서 조금 더 발전된 형태인데, 도식화하면 아래와 같다.
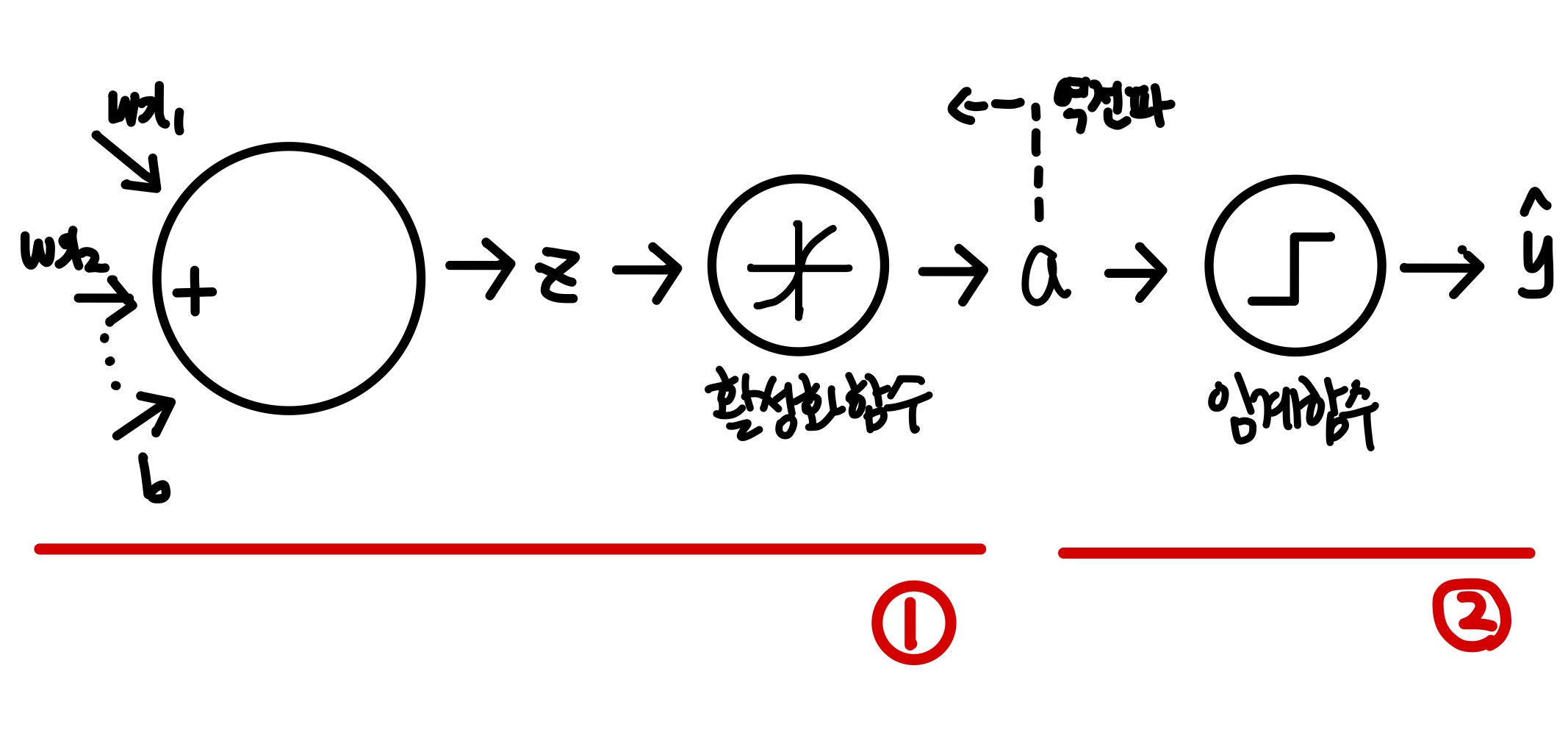
① 선형함수 & 활성화함수
로지스틱 회귀는 선형함수를 통과시켜 얻은 z값을 임계함수에 보내기 전에 변형시킨다.
이 변형시키는 함수를 활성화함수(activation function)이라고 부른다.
활성화함수의 특징 2가지를 살펴보자.
특징 1. 알고리즘별로 적합한 활성화함수가 있다.
활성화함수는 로지스틱 회귀 뿐만 아니라 다른 알고리즘에서도 사용하는 개념이다.
다만 알고리즘별로 적합한 활성화함수가 존재하는데, 로지스틱 회귀에 경우에는 시그모이드 함수를 사용한다.
시그모이드 함수는 아래와 같다.

로지스틱 회귀에서 시그모이드를 사용하는 이유는
무한대의 범위를 가지는 z값(선형회귀의 결과값)을 0~1사이의 확률값으로 변환시키기 위함이다.
이렇게 나온 확률값을 토대로 이진분류가 이뤄진다.
시그모이드 함수의 그래프는 아래와 같다.

그래프를 보면 어떤 z값이 들어와도 0~1 사이의 값이 출력된다.
특징 2. 활성화함수는 비선형함수를 사용한다.
활성화함수가 선형함수라면 앞쪽에 있는 선형함수와 (z를 만들어내는) 덧셈과 곱셈의 결합법칙과 분배법칙에 의해 다시 하나의 큰 선형함수로 정리할 수 있기 때문이다.
이렇게 되면 임계함수 앞에 뉴런을 여러개 쌓아도 결국 선형함수일 것이므로 의미가 없다.
따라서 활성화함수는 비선형함수를 사용한다.
② 임계함수
로지스틱 회귀는 마지막 단계에서 임계함수(Threshold function)을 사용하여 예측을 수행한다.
임계함수는 계단함수와 역할은 비슷하지만 0~1 사이의 확률값에 따라 0 또는 1로 구분한다는 점이 차이점이다.
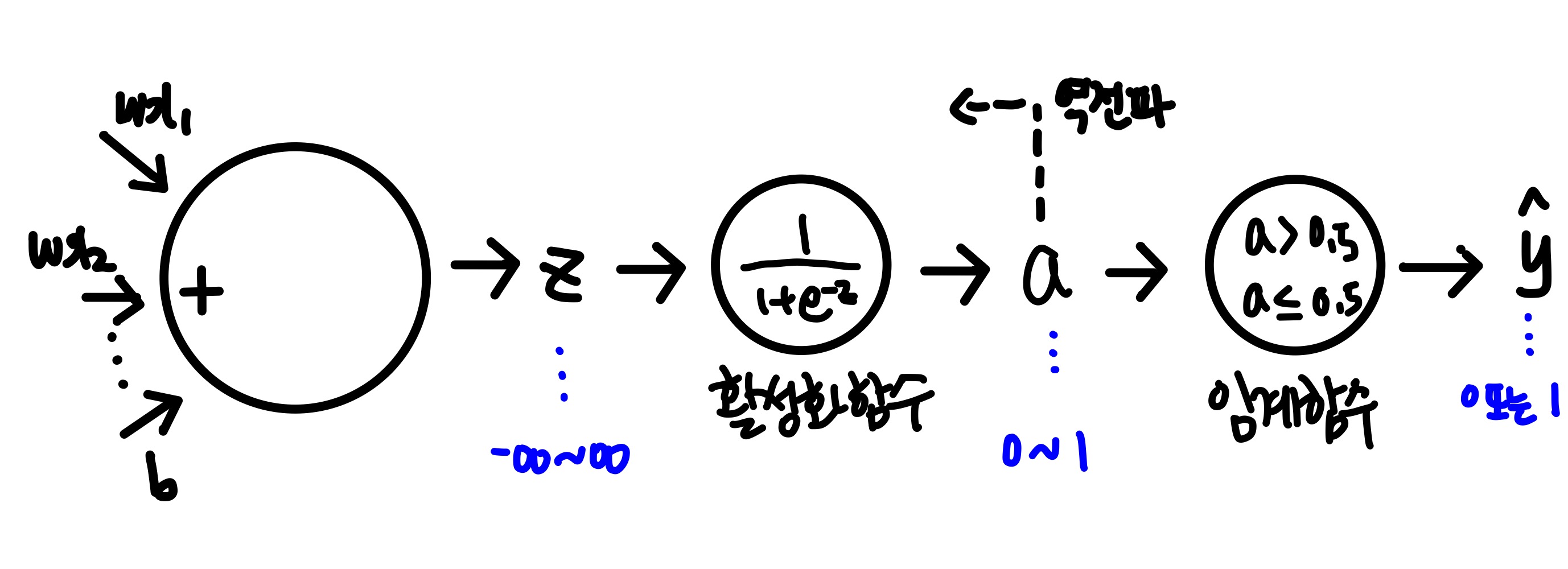
정리하면, 로지스틱 회귀는 이진분류가 목표이므로
-무한대부터 +무한대까지의 범위를 가지는 z의 값을 조절할 방법이 필요했다.
그래서 시그모이드 함수를 활성화 함수로 사용했다.
시그모이는 함수를 통과하면 z를 확률처럼 해석할 수 있기 때문이다.
그리고 시그모이드 함수의 확률인 a를 0과 1로 구분하기 위해서 마지막에 임계함수를 사용했다.
그 결과 입력데이터는 0또는 1의 값으로 분류, 즉 이진분류가 되었다.
'Deep Learning > [Books] Do it! 정직하게 코딩하며 배우는 딥러닝 입문' 카테고리의 다른 글
| [데이터 탐색] 데이터 탐색에 유용한 함수 2탄 - boxplot(), unique() (2) | 2020.07.16 |
|---|---|
| [모델 구축] 로지스틱 손실함수와 오류 역전파 이해하기 (0) | 2020.07.13 |
| [모델 구축] 선형회귀 알고리즘 구현하기 (전체 소스코드 첨부) (3) | 2020.07.06 |
| [데이터 탐색] 데이터 탐색을 위한 파이썬 명령어 3가지 (1) | 2020.07.02 |
| [모델 구축] 경사하강법을 구현하는 방법 - ② 손실함수 미분하기 (7) | 2020.06.29 |