
이번 포스팅에서는 과대적합을 해결하는 방법 중 하나인 '가중치 제한'을 다룬다. 가중치 제한이란 모델 훈련과정에서 가중치의 수정 범위를 제한하는 기법을 말한다. 그럼 먼저, 가중치의 수정범위를 제한하는 것이 어떻게 과대적합을 해결해주는지 부터 알아보자.
이 그래프, 성능이 높다고 말할 수 있을까?

이 그래프는 샘플 데이터 6개에 너무 집착한 나머지 박스로 표시한 샘플 데이터를 제대로 표현하지 못하고 있다. 모델이 몇개의 데이터에 집착하면 새로운 데이터에 적응하지 못하므로 좋은 성능을 가졌다고 말할 수 없다. 이런 모델은 훈련세트에서는 높은 성능을 낼지 모르지만 검증세트, 테스트세트에서는 높은 성능을 내기 어렵다. 즉 과대적합이 발생하는 것이다.
가중치의 수정범위를 조절한다는 것은 모델이 훈련데이터에 대해서 얼마나 정밀하게 그래프를 그릴 것이냐를 결정하는 것이다. 가중치 제한 정도가 작다면 훈련데이터에 밀착한 그래프를 그릴 수 있다. 반면 제한 정도가 크다면 훈련데이터에 맞는 그래프를 그리지 못할 것이고 과대적합을 해결할 수 있다. 하지만 제한 정도가 높으면 그래프의 정밀도가 떨어지는 만큼 과소적합이 발생할 가능성도 높기 때문에 데이터셋과 모델의 특징에 맞게 적합한 규제정도를 탐색하는 과정이 필요하다.
가중치를 규제하는 2가지 방법 : L1규제와 L2규제
L1규제
L1규제는 손실함수에 가중치의 절댓값을 더하는 방법이다. 이 가중치의 절댓값을 L1 노름(norm)이라고 하는데, 정의는 아래와 같다.

그럼 지난 포스팅에 이어서 로지스틱 손실 함수에 L1규제를 적용해보자. 이때 L1 노름을 그냥 더하지 않고 규제의 양을 조절하는 파라미터 알파(α)를 곱한 후 더한다.

※ 알파(α)가 규제의 양을 조절하는 원리?
인공지능 모델은 손실함수의 값이 작아지는 방향으로 가중치를 수정한다. 손실함수가 작아지기 위해서는 알파의 값이 클 때는 가중치 값의 합이 작아져야한다. 반면에 알파의 값이 작을 때는 가중치 값의 합이 커져도 손실함수의 값이 큰 폭으로 커지지 않는다. 이는 가중치 값이 큰 폭으로 커지거나 작아질 수 있다는 것을 의미한다. 이렇게 알파의 값을 조정하여 가중치 규제 정도를 조저할 수 있다.
나는 경사하강법으로 가중치를 업데이트하기 위해 L1규제를 적용한 로지스틱 손실함수를 미분하고 이를 가중치 업데이트 식에 적용했다. 이때, sign(w)는 w의 부호라는 의미의 함수이다.

L2규제
L2 규제는 손실함수에 가중치에 대한 L2 노름의 제곱을 더한다. L2 노름은 아래와 같이 정의한다.

다음으로 L1 규제와 동일하게 손실함수에 L2규제를 적용했다. 알파는 L1 규제와 마찬가지로 규제의 양을 조절하기 위한 매개변수이고, 1/2은 미분 결과를 보기 좋게 하기 위해 추가한다.
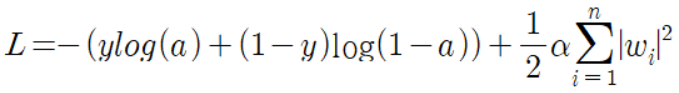
마지막으로 손실함수를 미분한 결과를 가중치 업데이트 식에 적용한다.

L1 VS L2
L2 규제의 가중치 업데이트 식을 보면 업데이트 과정에 가중치의 크기가 직접적으로 영향을 미치는 것을 알 수 있다. 가중치의 크기가 직접 영향을 미치기 때문에 L2 규제가 L1 규제 보다 가중치 규제에 좀 더 효과적이라고 한다. (정확한 이유는 조금 더 공부가 필요..) 그래서 L2 규제가 L1 규제보다는 널리 쓰이는 규제 방식이다.
Practice!
이전 포스팅에 구현했던 로지스틱 회귀 모델에 L1규제와 L2 규제를 반영할 수 있도록 소스를 수정했다. 그리고 규제를 하나도 적용하지 않았을 때의 정확도를 구해보았다.
class SingleLayer :
def __init__(self, learning_rate=0.1, l1=0, l2=0) :
self.w = None
self.b = None
self.losses = []
self.val_losses = []
self.lr = learning_rate
self.l1 = l1
self.l2 = l2
...(중략)...
def fit(self, x, y, epochs=100, x_val=None, y_val=None) :
self.w = np.ones(x.shape[1])
self.b = 0
for i in range(epochs) :
loss = 0
indexes = np.random.permutation(np.arange(len(x)))
for i in indexes :
z = self.forpass(x[i])
a = self.activation(z)
err = -(y[i] - a)
w_grad, b_grad = self.backdrop(x[i], err)
w_grad += self.l1 * np.sign(self.w) + self.l2*self.w
self.w -= self.lr * w_grad
self.b -= b_grad
a = np.clip(a, 1e-10, 1-1e-10)
loss += -(y[i]*np.log(a) + (1-y[i])*np.log(1-a))
self.losses.append(loss/len(y) + self.get_loss())
self.update_val_loss(x_val, y_val)
def get_loss(self) :
return self.l1 * np.sum(np.abs(self.w)) + self.l2/2 * np.sum(self.w**2)
...(중략)...
def update_val_loss(self, x_val, y_val) :
if x_val is None :
return
val_loss = 0
for i in range(len(x_val)) :
z = self.forpass(x_val[i])
a = self.activation(z)
a = np.clip(a, 1e-10, 1-1e-10)
val_loss += -(y_val[i]*np.log(a)+(1-y_val[i])*np.log(1-a))
self.val_losses.append(val_loss/len(y_val) + self.get_loss())
...(중략)...
LayerNone = SingleLayer()
LayerNone.fit(x_train_scaled, y_train)
LayerNone.score(x_val_scaled, y_val)
# 결과 : 0.967032967032967
다음으로 L1의 규제 정도가 0.0001, 0.001, 0.01일 때 훈련세트와 검증세트의 에포크별 손실함수 추이 그래프를 그려보았다.
import matplotlib.pyplot as plt
l1_list = [0.0001, 0.001, 0.01]
for l1 in l1_list :
lyr = SingleLayer(l1=l1)
lyr.fit(x_train_scaled, y_train, x_val = x_val_scaled, y_val = y_val)
plt.ylim(0,0.3)
plt.plot(lyr.losses)
plt.plot(lyr.val_losses)
plt.ylabel('loss')
plt.xlabel('epoch')
plt.legend(['train_loss', 'val_loss'])
plt.show()
plt.ylim(-4,4)
plt.plot(lyr.w, 'bo')
plt.title('Weight(l1={})'.format(l1))
plt.ylabel('value')
plt.xlabel('weight')
plt.show()
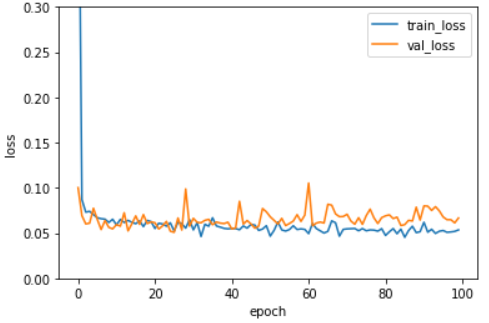
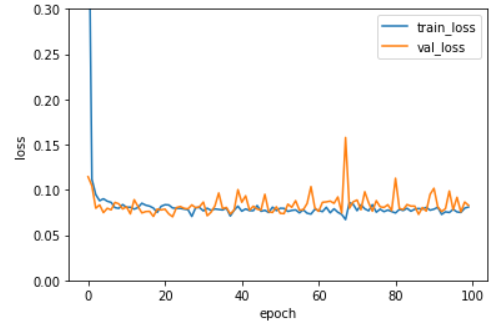

학습곡선 그래프를 보면 규제가 커질수록 훈련세트의 손실과 검증세트의 손실이 모두 높아진다. 즉 과소적합 현상이 발생한다. 규제정도가 아주 적은 l1 = 0.0001은 20회 에포크부터 훈련세트의 손실함수 값이 검증세트의 손실함수 값보다 작아지는 과대적합 현상이 발생하므로, l1 = 0.001 정도가 가장 적합해보인다. 이 값을 사용하여 새로운 모델을 만들어 성능을 확인해보았다. 에포크는 l1 = 0.001에서 검증세트의 손실함수가 훈련세트의 손실함수보다 커지기 전인 40회로 설정했다.
layerL1 = SingleLayer(l1=0.001)
layerL1.fit(x_train_scaled, y_train, epochs=40)
layerL1.score(x_val_scaled, y_val)
# 결과 : 0.967032967032967
규제를 적용하지 않았을 때와 동일한 성능이 나왔다. 다음으로 L2 규제를 사용해 그래프를 그려보았다.
l2_list = [0.0001, 0.001, 0.01]
for l2 in l2_list :
lyr = SingleLayer(l2=l2)
lyr.fit(x_train_scaled, y_train, x_val = x_val_scaled, y_val = y_val)
plt.ylim(0,0.3)
plt.plot(lyr.losses)
plt.plot(lyr.val_losses)
plt.ylabel('loss')
plt.xlabel('epoch')
plt.legend(['train_loss', 'val_loss'])
plt.show()
plt.ylim(-4,4)
plt.plot(lyr.w, 'bo')
plt.title('Weight(l2={})'.format(l2))
plt.ylabel('value')
plt.xlabel('weight')
plt.show()
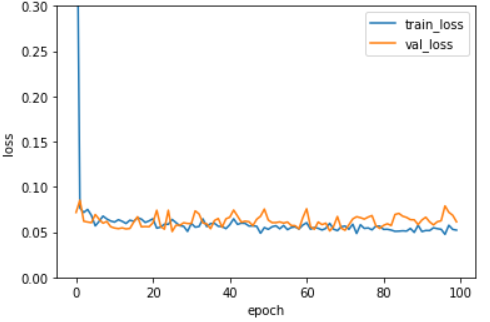
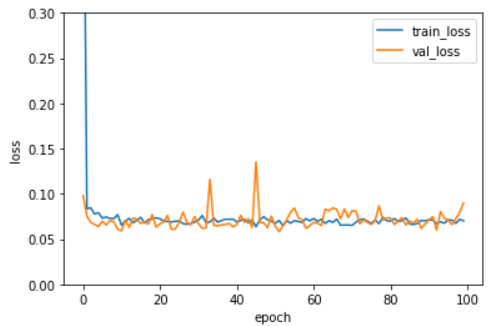

L1 규제와 비슷한 양상을 보이기는 하지만 규제 강도가 강해져도 L1 규제만큼 과소적합이 심해지지 않는 것을 확인할 수 있었다. L2 규제 역시 규제가 작을 때는 과대적합 현상이 발생했으므로 l2=0.001의 규제를 사용하여 성능을 평가했다. l2=0.001일 때 전반적으로 훈련세트와 검증세트의 손실함수 값이 유사한 경향을 띄기 때문에 에포크 횟수는 100회로 설정했다.
layerL2 = SingleLayer(l2=0.001)
layerL2.fit(x_train_scaled, y_train, epochs=100)
layerL2.score(x_val_scaled, y_val)
# 결과 : 0.967032967032967Conclusion.
| 모델 | L1 | L2 | epoch | 정확도 |
| LayerNone | - | - | 100 | 0.967032967032967 |
| LayerL1 | 0.001 | - | 40 | 0.967032967032967 |
| LayerL2 | - | 0.001 | 100 | 0.967032967032967 |
과대적합은 해결했지만 규제를 적용한 모델의 성능이 높지는 않았다. 원인을 추론해보면 데이터 세트 수가 아주 적기 때문(위 경우 테스트세트의 수가 91개였다.)일 수 있다. 다음 포스팅에서는 이렇게 데이터 수가 작을 때 성능을 높일 수 있는 방법인 교차검증에 대해서 다뤄보겠다.
Reference.
도서 <Do it! 정직하게 코딩하며 배우는 딥러닝 입문> 이지스 퍼블리싱, 박해선 지음
끝.
'Deep Learning > [Books] Do it! 정직하게 코딩하며 배우는 딥러닝 입문' 카테고리의 다른 글
| Python으로 다층신경망 구현하기 (0) | 2020.10.12 |
|---|---|
| [모델 튜닝] K-폴드 교차검증 (1) | 2020.10.04 |
| [모델 튜닝] 하는 방법 - 과대적합과 과소적합 (6) | 2020.09.24 |
| [모델 튜닝] 머신러닝/딥러닝 Validation Set 만드는 이유와 방법 (0) | 2020.09.22 |
| [데이터 전처리] 스케일 조정 (2) | 2020.07.30 |